
ASAL SAYILAR
ASAL SAYILAR
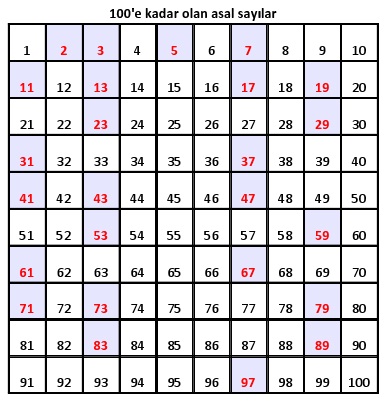
Yüzden küçük asal sayılar
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 ve 97 dir.
1'i asal sayı olarak kabul ediyorlardı ve 1'in asal olarak kabul edilmesine dayanarak yapılan birçok çalışma geçerliliğini hâlâ sürdürmektedir.Örneğin Stern ve Zeisel'in çalışmaları.Henri Lebesgue, çalışmalarında 1'i asal olarak ele alan son profesyonel matematikçi olarak bilinir.
1'i asal olarak ele alırsa bazı teoremlerde değişikliğe gidilmesi gerekir.
Örneğin tüm pozitif tam sayıların "yalnız bir şekilde" asal sayıların çarpımları şeklinde yazılabileceğini söyleyen Aritmetiğin temel teoremi, nitekim geçmişteki asal sayı tanımına göre geçerli değildir.
19. yüzyıla kadar birçok matematikçi 1`i asal sayı olarak kabul etmiş olsa da bugün `0` ve `1` asal sayı kabul edilmez.
Çünkü, `0` kendisine bölünemez, `1` sayısı ise, sadece kendine bölünebildiği için asal sayı olarak kabul edilemez.
Öklid (Euklides)'ten beri asal sayılar sonsuz olduğu bilinmektedir, fakat asal sayılar hakkında pek çok başka soru hala daha cevapsızdır. Bunlardan en ünlü ikisi aralarındaki fark iki olan asal sayılar (örneğin 11 ve 13, veya 29 ve 31) hakkındaki ikiz asallar konjektürü ve asal sayıların doğal sayılar içersindeki dağılımı hakkındaki Riemann Hipotezidir.
Sayılar teorisi'nin en önemli uğraşı asal sayılar hakkındaki bu tür sorulardır.
Asal sayılarla ilgili Goldbach hipotezi halen kanıtlanamamıştır:
Her çift sayı iki asal sayının toplamı mıdır?
Örneğin:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5...
İKİZ ASALLAR
Aralarındaki fark 2 olan asal sayılara ikiz asal sayılar denir. (örneğin 3 ve 5, 5 ve 7, 11 ve 13 .. ikiz asallardır.) (2, 3) çifti hariç iki asal sayının arasındaki fark da zaten en az 2 olabilir.
İkiz asalların sonsuz tane olmasına ilişkin soru , sayılar kuramının yıllardır çözülememiş en büyük problemlerinden birisidir ve "ikiz asallar sanısı ( varsayımı, kestirimi) olarak adlandırılır. 3'ten büyük her ikiz asal sayı çifti, bazı n doğal sayıları için, (6n-1 , 6n +1) şeklinde ifade edilir. Öyleki n, 1'e eşit değildir ve 0, 2, 3, 5, 7 veya 8 ile sonlanmak zorundadır.
İlk 35 ikiz asal sayı çifti
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
EN BÜYÜK ASAL SAYI
2008 yılında keşfedilen 12.978.189 basamaklı en uzun asal sayı rekoru, 17.425.170 basamaklı yeni asal sayının bulunmasıyla geçildi. Internet Mersenne Prime Search (GIMPS)(Mersenne Asalları Büyük İnternet Araştırması) projesindeki gönüllüler ile Missouri Üniversitesi'nde görevli olan Dr. Curtis Cooper, bugüne kadar bilinen en büyük Mersenne asal sayısını keşfetti.
257,885,161-1 (2^57,885,161-1) şeklinde yazılan 48'inci Mersenne sayısı, GIMPS projesindeki bilgisayar ağı kullanılarak hesaplandı. 17 milyon basamaklı bir sayı ile 28 adet roman uzunluğunda kitap yazılabiliyor. En Büyük Asal Sayı Kaçtır? Öklid (Euklides)'ten beri asal sayıların sonsuz olduğu kabul edilir.
Asal sayılar hakkındaki pek çok soru günümüzde hâlâ cevaplanamamaktadır. Asırlardır asal sayılar üzerinde bir çok teorem ortaya atılmış, asal sayıların bulunması için çeşitli formüller üretilmeye çalışılmıştır. Fakat bunların hepsinin yanlış olduğu kanıtlanmıştır. Günümüzde asal sayıları veren bir matematik formülü bulunmamaktadır. Sayılar Teorisi'nin en önemli uğraşısı asal sayılar hakkındaki bu tür sorulardır. Asal sayılar ayrıca Kriptografi alanının da yapı taşlarıdır.
Bilinen En Büyük Asal Sayı:
257,885,161-1
KAÇ TANE ASAL SAYI VARDIR?
Kendisinden ve birden başka hiçbir tam sayıya bölünemeyen sayılara asal sayı deriz. Örneğin 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 asal sayılardır. Asal sayıların listesini çıkarmaya başladığınız zaman listedeki sayıların arasının genellikle açılmaya başladığını görürsünüz.
Örneğin 1 ile 100 arasında yirmibeş asal sayı varken 100 ile 200 arasında yirmibir asal vardır. Daha büyük aralıklara bakarsak örneğin 1 ile 1 milyon arasında 78498 asal sayı varken 10 milyon ile 11 milyon arasında 61938 asal vardır. Buna bakarak asalların azaldığını ve giderek yok olacağını dü_şünebilirsiniz.
Bu durumda doğal olarak en büyük asal sayı hangisidir, diye bir soru sorabilirsiniz. İşte 2000 yıl önce Öklid bu soruya çok şık bir cevap vermiştir. Öklid en büyük asal diye bir sayının olmadığını, asal sayılar listesinin sonsuz olduğunu iddia etmiştir. Bir an için Öklid asal sayılar listesinin sonlu olduğunu kabul eder.
Buna göre p1 < p2 < ... < pn elimizdeki bütün asallar olsun. Şimdi K=p1.p2 ... pn + 1 sayısını düşünelim.
Bu sayı elimizdeki asal sayılar listesindeki her asaldan farklıdır. Var olan tüm asallar bu listede olduğuna ve K sayısı bu listede olmadığına göre K sayısı asal değildir.
Öyleyse elimizdeki listedeki asallardan en az biri tarafından bölünmeli. Oysa K sayısı bu asallardan hiç birine bölünmez. Örneğin K= 1 + p1 . (p2 ... pn) şeklinde yazıldığı için p1 asalına böldüğümüz zaman 1 artar. Aynı nedenle diğer asallara da bölünmez. Bir çelişkiye vardık. Asal sayıların sonlu sayıda bulunduğunu varsayınca açık bir çeliş_ki elde ediyoruz. Demek ki asal sayılardan sonsuz tane var. Bu kadar basit. Şimdi bu duruma itiraz edebilirsiniz. Bu elde ettiimiz K sayısını da listeye ekleseydik çelişkiden kurtulur muyduk? Dikkat ederseniz çelişkiyi elde etmemizin nedeni K sayısının listede olup olmamasından çok listede yalnızca sonlu sayıda asal olmasıydı.
Eğer listede sonlu sayıda asal olmasaydı onları birbiriyle çarpıp 1 ekleyerek bir K sayısı elde edemez ve çelişki bulamazdık. Çelişki K sayısından değil, asalların listesinin sonlu varsayılmasından doğdu. Asal sayılarla oynamak büyük bir zevk kaynağıdır.
Örneğin her n sayısıyla 2n sayısı arasında mutlaka bir asal olduğunu gösterebilir misiniz? Bu bilinen bir sonuçtur ama ispatı biraz çetrefillidir. Ya da üçten büyük her çift sayının iki asalın toplamı olarak yazılabileceğini gösterebilir misiniz?
Bu Goldbach önermesi olarak tanınır ve hala doğru olup olmadığı bilinmemektedir. Ölümlü insanların bugüne kadar deneyebildikleri her çift sayı için önermenin doğru çıktıını söylemeye gerek yok...
Ama ya henüz deneyemediğimiz büyüklükteki bir çift sayı için yanlışsa...
ASAL SAYILAR VE ŞİFRELEME ( KRİPTOLOJİ )
Kriptoloji, şifre bilimidir. Çeşitli iletilerin, yazıların belli bir sisteme göre şifrelenmesi, bu mesajların güvenlikli bir ortamda alıcıya iletilmesi ve iletilmiş mesajın deşifresiyle uğraşır. Asal sayılar özellikle internet üzerinden yapılan işlemlerin güvenli bir şekilde yürümesine olanak tanıyan şifreleme tekniklerinin geliştirilmesi için kullanılıyor. Her ne kadar günümüzde bankacılıkta kullanılan şifreleme teknikleri için UCLA`lı matematikçilerin bulduğu kadar çok basamaklı büyük sayılara ihtiyaç duyulmasa da, askerî bilgiler gibi önemli şifrelemeler gerektiren verilerin korunmasında kullanılacak asal sayıların olabildiğince fazla basamaklı olması gerekiyor. RSA Şifreleme Algoritması RSA algoritması, Amerika’ da 1983 yılında MIT’ten patent almıştır. Bu patent 21 Eylül 2000 de son bulmuştur. Ancak patenti daha önce bir uygulamaya ait olduğu için bir başka ülkede patent alınamaz. Bir genel anahtarlı şifreleme tekniği olan RSA, çok büyük tamsayıları oluşturma ve bu sayıları işleminin zorluğu üzerine düşünülmüştür. Anahtar oluşturma işlemi için asal sayılar kullanılarak daha güvenli bir yapı oluşturulmuştur. Anahtar oluşturma algoritması şu şekildedir: • P ve Q gibi çok büyük iki asal sayı seçilir. • Bu iki asal sayının çarpımı N = P.Q ve bu bir eksiklerinin φ(N)=(P-1)(Q-1) hesaplanır. • 1’den büyük φ(N)’den küçük φ(N) ile aralarında asal bir E tamsayısı seçilir. • Seçilen E tamsayısının mod φ(N)’de tersi alınır, sonuç D gibi bir tamsayıdır. • E ve N tamsayıları genel anahtarı, D ve N tamsayıları ise özel anahtarı oluşturur. Genel ve özel anahtarları oluşturduktan sonra gönderilmek istenen bilgi genel anahtar ile şifrelenir. Şifreleme işlemi şu şekilde yapılmaktadır: Şifrelenecek bilginin sayısal karşılığının E’ ninci kuvveti alınır ve bunun mod N deki karşılığı şifrelenmiş metni oluşturmaktadır. Genel anahtar ile şifrelenmiş bir metin ancak özel anahtar ile açılabilir. Bu yüzden şifrelenmiş metin, yine aynı yolla, şifrelenmiş metnin sayısal karşılığının D’ninci kuvveti alınır ve bunun mod N deki karşılığı orijinal metni oluşturur. Basit bir örnek ile algoritmayı tekrar anlatalım. Örneğin basitliği açısından daha küçük asal sayılarla çalışacağız. Öncelikle genel ve özel anahtarlarımızı oluşturalım. • P=7 ve Q=17 gibi iki asal sayı seçelim. • Bu iki asal sayının çarpımı N=P.Q; N=119 ve bu iki asal sayının bir eksiklerinin çarpımı φ(N)=(P-1)(Q-1); φ(N)=96 olarak hesaplanır. • 1’den büyük 96’dan küçük 96 ile aralarında asal bir E=5 tamsayısı seçelim. • Seçilen E=5 tamsayısının mod 96’da tersi alınır, sonuç D=77 gibi bir tamsayıdır. • 5 ve 119 tamsayıları genel anahtarı, 77 ve 119 tamsayıları ise özel anahtarı oluşturur.
Bu algoritmada iki asal sayının çarpımını kullanarak anahtar oluşturulmasının sebebi, iki asal sayının çarpımını asal çarpanlarına ayırmak asal olmayan sayıları ayırmaktan daha zorlu olmasıdır.












